Stellar Magnitude

Austin Lee

Stellar Magnitude

                 Stellar Magnitude was created by the Greek astronomer Hipparchus to rank their brightness. First magnitude is the brightest, second magnitude is the second brightest, and so on. It is logarithmic; brightness increases by a fixed 2.5 times with each magnitude. It is measured on a logarithmic scale and not a linear scale because the human eye perceives stimuli logarithmically, meaning that perception increases by a fixed factor. This trait is called Fechner’s Law.

                   Because the Greeks believed the stars were all located on the same sphere around the earth, this was an easy way to classify stars for them. But because we have learned this is not the actual structure of the universe, modern astronomy amends the concept of magnitude to fit our model. We divide magnitude into two groups: apparent magnitude, which is a star’s perceived brightness from any viewpoint, and absolute magnitude, which is the intrinsic brightness of a star that never changes, measured at 10 parsecs from the star. The absolute magnitude and apparent magnitude can vary greatly depending on the distance of the star from Earth. Vega is used as a reference scale for magnitude, marked at 0, and brightness increases in the negatives. Our sun on the scale has a very bright apparent magnitude of -26.74 because it is obviously the closest star to us, but only an absolute magnitude of 4.83, which is average.

 

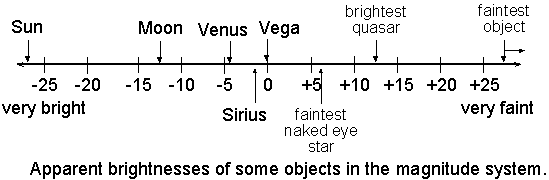
Chart courtesy of http://www.astronomynotes.com/starprop/s4.htm

            As per the graph, the faintest naked eye star is a little past 5 on the apparent brightness scale. At 2, stars become hard to see in small cities. At 3, they are still barely visible in small cities but densely lit urban areas need binoculars to see the star. By 4, only the suburbs can see the star.

            By comparing the absolute magnitude (M) and apparent magnitude (m) of a star, we can determine our distance from the star. The difference between them (m-M) is called the distance modulus. A distance modulus of 0 means the star is 10 parsecs away, and a negatively increasing distance modulus means it is closer, and a positively increasing distance modulus means it is further away.